

The general rule of transformation of rotation about the origin is as follows. The shape rotates counter-clockwise when the number of degrees is positive and rotates clockwise when the number of degrees is negative. The transformation that rotates each point in the shape at a certain number of degrees around that point is called rotation. The transformation of f(x) is g(x) = - x 3 that is the reflection of the f(x) about the x-axis. Here is the graph of a quadratic function that shows the transformation of reflection. Thus the line of reflection acts as a perpendicular bisector between the corresponding points of the image and the pre-image. If point A is 3 units away from the line of reflection to the right of the line, then point A' will be 3 units away from the line of reflection to the left of the line. Every point (p,q) is reflected onto an image point (q,p). When the points are reflected over a line, the image is at the same distance from the line as the pre-image but on the other side of the line. The type of transformation that occurs when each point in the shape is reflected over a line is called the reflection. The transformation f(x) = (x+2) 2 shifts the parabola 2 steps right. This pre-image in the first function shows the function f(x) = x 2. We can apply the transformation rules to graphs of quadratic functions. This translation can algebraically be translated as 8 units left and 3 units down. 3 units below A, B, and C respectively.8 units to the left of A, B, and C respectively.
We need to find the positions of A′, B′, and C′ comparing its position with respect to the points A, B, and C. To describe the position of the blue figure relative to the red figure, let’s observe the relative positions of their vertices. Translation of a 2-d shape causes sliding of that shape. Transformations help us visualize and learn the equations in algebra. We can use the formula of transformations in graphical functions to obtain the graph just by transforming the basic or the parent function, and thereby move the graph around, rather than tabulating the coordinate values. Transformations are commonly found in algebraic functions. Transformations can be represented algebraically and graphically.
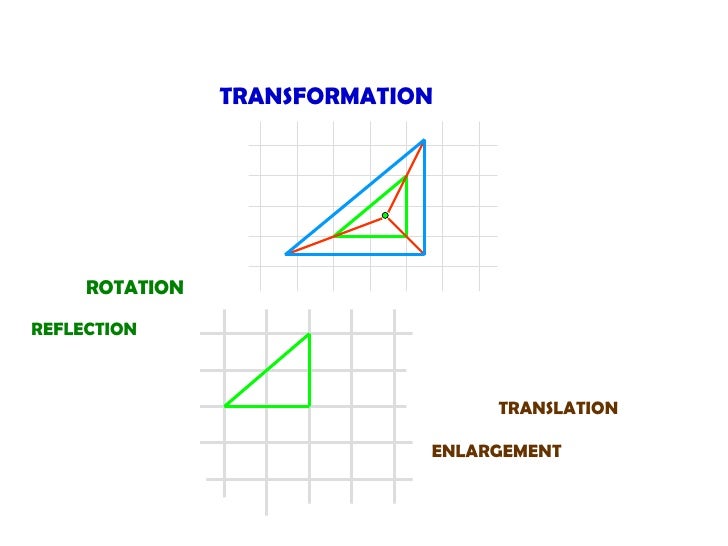
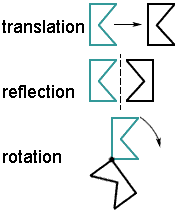
Here are the rules for transformations of function that could be applied to the graphs of functions. On a coordinate grid, we use the x-axis and y-axis to measure the movement. Enlarge the triangle by a scale factor of 2.Consider a function f(x). If the scale factor is 1/2, draw lines which are 1/2 as long, etc. If the scale factor is 3, draw lines which are three times as long. Measure the lengths of each of these lines.Ģ) If the scale factor is 2, draw a line from the centre of enlargement, through each vertex, which is twice as long as the length you measured. The resultant position of the shape on the tracing paper is where the shape is rotated to.Įnlargements have a centre of enlargement and a scale factor.ġ) Draw a line from the centre of enlargement to each vertex ('corner') of the shape you wish to enlarge. Push the end of your pencil down onto the tracing paper, where the centre of rotation is and turn the tracing paper through the appropriate angle (if you are not told whether the angle of rotation is clockwise or anticlockwise, it would usually be anticlockwise). If you wish to use tracing paper to help with rotations: draw the shape you wish to rotate onto the tracing paper and put this over shape. When describing a rotation, the centre and angle of rotation are given. The distance of each point of a shape from the line of reflection will be the same as the distance of the reflected point from the line.įor example, below is a triangle that has been reflected in the line y = x (the length of the pink lines should be the same on each side of the line y=x): When describing a reflection, you need to state the line which the shape has been reflected in. A reflection is like placing a mirror on the page.


 0 kommentar(er)
0 kommentar(er)
